CODE FESTIVAL 2014 本戦
2014-11-14 | [Competitive programming]本戦前
1 位をとっても税金があぶなくならないことを確認しておく
day 1
- 適当に会場まで行く
- 会場までの道が難しい
本戦
- A, B, C, D, E は簡単なので普通に解いた
- F からいきなり難しくなってびっくりする
- 最初 F 解ける気がしなかったので G (加法的 3 * 3 魔法陣の列の和が中心の 3 倍になることは有名事実なのでひっかかってしまった) を解きに行く
- 全探索するけど全然通らない…
- あまり通らないのであきらめて F を考える
- バグ出しまくったけどなんとか通す
- 一旦 G あきらめて H を読む
- 少し考えたら、常に部屋の人数は高々 3 種類しかないことに気づいたので適当にやって通す
- I を読んだら、最初読んだときはなぜか幾何に見えて敬遠していたがよく読んだら離散系でしかもデータ構造なので書き始める
- つまらない配列あふれを起こすもなんとか通す
- その後は G や J を考える
- J 解けそうな形になって、書いてみるもサンプルが合わない
- WA 無限回生やしていいコンテストなのでいい加減な修正をかけて送る → WA
- バグに気づいて直して送る → WA (しかもテストケース 1 個を除いて AC)
- ここらへんでコンテスト終了><
- 少し考えたら、あまりにも自明なケース (K = 0) で落ちていることが判明…
- それ直したら通ってしまった
- G に着手したり J で自明なケースで落として結局通せないとかけっこうひどいことやったけどなんとか 1 位だった
- 入力ゲーとか悪質なデバッグゲーとかもなく普通に楽しめる問題セットだった
本戦後
- あまり時間がないので適当にめしとか DDR とかタイピングとかした
- タイピングむずかしい (>_<)
- タイピング記録抜かれている (しかも 10 秒とかいうレベルで) ことがわかって、なんとしても追い越したくなる (エキシビションのためその時は時間なかった)
エキシビションマッチ
- とりあえず両方の問題を見る。さすがにどっちも難しい
- A を考えてみる
- なんとなく移動可能性で連結成分とるとよさそうだなーとなる (さすがに連結成分内でラベルの集合が一致してないとだめ)
- それだけだと自明な反例が構成できたので、連結成分ごとに偶置換であることも必要そうだなーとなる
- (当然のことながら、明確な根拠なしに) この 2 つの条件だけで必要十分っぽく見えたので書く
- 通った
- B をまじめに考える
- 挿入位置があらかじめわかれば使わない位置には 0 とか入れておけば Starry Sky 木で解けそうに見えたけど挿入位置がわからない
- まさか平衡木とか書きたくないので、「平衡木が必要そうなときに使う一般的なテク」の平方分割を検討する
- 計算量大丈夫そうなので書き始める
- とりあえず書けたので送るが、さすがに一発で通るわけもなく WA
- バグだらけだったのでいろいろ直して送るも通らない
- pool を大きくしてもだめ
- 中身のなくなったバケットを消去するようにしてもだめ
- 結局更新のとき vector を clear してないだけだった
- 終了 1 分前に通る
- このとき体育館がだいぶ盛り上がっているのが聞こえた
- エキシビションマッチは観戦したら面白そうだなあ、と思ってたけど contestant のほうでも普通に面白かったし体育館のほうも盛り上がってたようでよかった
- コンテスト中体育館どんな感じだったのか見たい
夜
- ホテルに移動
- ホテルかなりよかった (トイレのドアが透明なのは謎だった)
- コンビニやゲーセン行ったり部屋でネットしたりして寝る
day 2
あさ
- おきてホテルでめし。朝食のところで筑波の人と話した
- 会場へ移動
- まためしを食べる (さすがにそんなに食べられなかった)
あさプロ
- 普通に A 問題から見る
- 適当にバイナリ法っぽくやったら通った
- B 問題を考える
- 普通の DP だった
- 送る。 WA
- なんでや、と思ったら境界を微妙にまちがえていた
- 直して AC
- C 問題
- 平方分割だろうと思ったらどう考えても計算量やばいことがわかって絶望する
- よく考えたら隣接する箇所しか更新しないし imos 法テーブルで更新すべきところ少ない
- 書いて通す
- D 問題、幾何で (>_<) となる
- やるべきことは単にスネルの法則っぽい
- ちょうど幾何ライブラリ入ってたし気合で書いてサンプル合わせる
- WA
- EPS けっこう厳しくてやばそうだったのでゆるくして送る
- TLE
- O(E log V) の Dijkstra は密グラフに対しては相当遅いという事実を思い出す
- 隣接行列を使って O(V^2) のコードを書く
- MLE
- 配列の範囲をぎりぎりに減らす
- ようやく通った
- 30 分余ったので複素解析した
昼
- めし食べる
- DDR 空いていることをいいことに何回もやる (最初難易度の変更方法がわからず自明しか遊べなかった)
- タイピングなんとしても勝ちたかったので何回もやって最終的に 100ms 差で勝つ
- りんごさんの LT (高橋君について、と風船釣り) がやばかった
- あとはボードゲームのところを見たりする
リレー
- 体育館に入る
- 「机の上のものは触ってはいけない」とだけ言われたので覗きこむことは差し支えないだろう、という理屈のもとルールの紙を読む
- ルール難しい (>_<)
- とりあえずチームで順位順に担当を決めて解くことにしたけど J が全然わからない…
- このときは本気でエキシビションの問題より難しいと思っていた
- 制約を見て O(N^4) の DP っぽいとかいい加減なことを考えてしまう
- J わからないうちに結局他の問題全部解かれてしまいパソコンの前で考えるほかなくなる
- 全然わからない…
- しかも放送が煽ってくるのでまったく集中できない
- そうこうしているうちにどんどん J 問題が解かれて焦る
- チームの机に行ってなにかヒントっぽいものがないか聞く
- 偶奇と K の大きさで場合分けすればよさそう?みたいなことを聞いたので書く
- 通る
- 難しい DP の類かと思っていたので完全に拍子抜けだった
- 結局完全に戦犯になってしまってつらい
- 「チーム対抗リレー」という情報をまったく使えなかったのが敗因かなあ…
- 最終問題で Div1Hard とか出しても全部のチームが通せるわけない
- そういうの出すと結局個人戦に帰着されてしまうのでどのチームでも通せうるレベルの問題しか出ない、というところまで考えるべきだった
- そもそもパソコンが使えるんだから O(2^N*N^2) 書いて実験するべきだった…
- 嘘解法生やしてしまうとだいぶつらくなるルールだなあと思った
まとめ
- とても楽しかったし来年開催されたらまた行きたい
補遺 : エキシビション A の必要十分性の証明
- 必要十分条件は「すべての番号の行き先が、同じ三角形辺連結成分内にある」「すべての連結成分内で、番号の入れ替えが偶置換になっている」であることを示す
- これが必要条件であることは自明
- 十分性を連結成分ごとに示す
- 同じ連結成分では、任意の 3 点に対して、その 3 点に対する回転を行うのと同等の操作列が構成できることの証明
- 連結成分の大きさの数学的帰納法で示す
- 大きさが 3 のときは、単に三角形があるだけなので自明
- 大きさが n の部分 P に対して、新たな 1 or 2 点を三角形でつないで付け加える
- 1 点を付け加える場合
- つなぐ三角形は、P と 2 点を共有し、共有辺を持つ
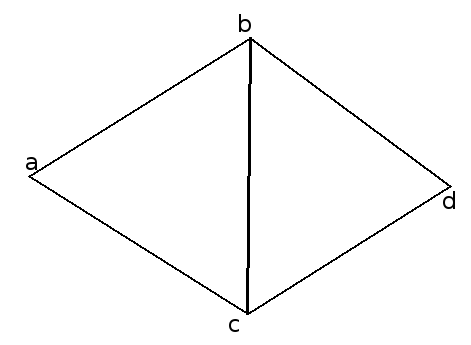
- a, b, c が P に含まれ、d が新たな点とする
- a, b, d の回転を構成すれば十分
- 左の三角形を反時計回りに 1 回、右の三角形を時計回りに 1 回回転することにより構成できる
- つなぐ三角形は、P と 2 点を共有し、共有辺を持つ
- 2 点を付け加える場合
- つなぐ三角形は、P と 1 点を共有する
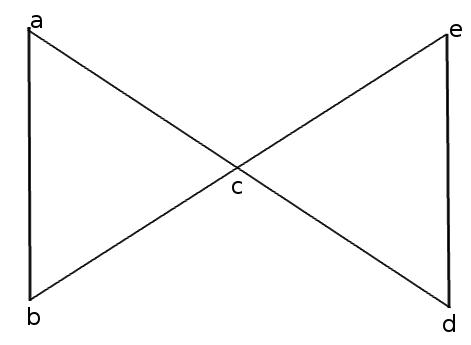
- a, b, c が P に含まれ、d, e が新たな点とする
- a, c, e の回転と a, d, e の回転を構成すれば十分
- a, c, e の回転は、
- 左の三角形を反時計回り
- 右の三角形を時計回り
- 左の三角形を時計回り
- 右の三角形を反時計回り
- に 1 回ずつこの順で回転することより構成できる
- a, d, e の回転は、
- 左の三角形を時計回り
- 右の三角形を時計回り
- 左の三角形を反時計回り
- に 1 回ずつこの順で回転することにより構成できる
- つなぐ三角形は、P と 1 点を共有する
- 任意の 3 点に対して回転が行えるとき、任意の偶置換が構成できることの証明
- 1, …, n (n >= 3) の偶置換の列 s[i] (1 <= i <= n) が与えられて、これを回転のみにより整列させることができることを示せばよい
- i = 1, 2, …, n-2 に対して、順次以下を行う:
- s[i] = i なら何もしない。
- s[i] = j > i なら (アルゴリズムの過程で j < i となることはない) i, j および勝手な k (i < k, j != k) を選び、 i, j, k で回転を行って s[i] = i とする。
- この操作の後で、i = 1, 2, …, n-2 に対しては s[i] = i となる
- 一方 (s[n-1], s[n]) に対しては、(n-1, n) と (n, n-1) の両方の可能性が考えられるが、元の列が偶置換であり、回転操作は偶置換であることから、(n-1, n) である
- よって s[i] が回転操作のみで整列できた
- 同じ連結成分では、任意の 3 点に対して、その 3 点に対する回転を行うのと同等の操作列が構成できることの証明